Difference between revisions of "SL Helicopter Flying Handbook/Navigation"
(→Dead Reckoning) |
(→Dead Reckoning) |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 23: | Line 23: | ||
Dead reckoning, in the context of air navigation, is the process of calculating heading, speed and time to travel between fixed points given vehicle speed and wind conditions. While manual dead reckoning is not a common technique for SL navigation, it is useful for pilots to understand the basics, in particular when flying an aircraft with simulated wind. | Dead reckoning, in the context of air navigation, is the process of calculating heading, speed and time to travel between fixed points given vehicle speed and wind conditions. While manual dead reckoning is not a common technique for SL navigation, it is useful for pilots to understand the basics, in particular when flying an aircraft with simulated wind. | ||
| − | + | In the no-wind case, a pilot could simply use an aeronautical chart to measure the heading needed to fly from her current location to her destination, then calculate the time required as the distance divided by the airspeed. For example, to make a 30km flight at an airspeed of 60 kph would require 30 minutes. | |
| + | |||
| + | The presence of wind, can make things more complicated (for aircraft that support wind). When there is a direct tailwind, we can simply add the windspeed to the airspeed to get groundspeed, and when there is a direct headwind, we can simply subtract the airspeed. In the same example as above, if there is a 10 knot tailwind, then the groundspeed becomes 70 knots, and this the time to cover the 30 km flight would be 30/70 hours or 26 minutes. | ||
| + | |||
| + | Things can be more complicated still when the wind is not aligned with the direction of travel. In this case we must employ the wind triangle to calculate a heading and groundspeed. Before explaining the wind triangle, we make the following definitions: | ||
| + | |||
| + | * True Course - The course from a departure fix to a destination fix. | ||
| + | * Heading - The direction in which the aircraft is "pointing". | ||
| + | * Airspeed - The speed through the air as shown on the airspeed indicator. | ||
| + | * Groundspeed - The actual speed across the ground. | ||
| + | * Wind Correction - The difference between the true course and the heading. | ||
| + | |||
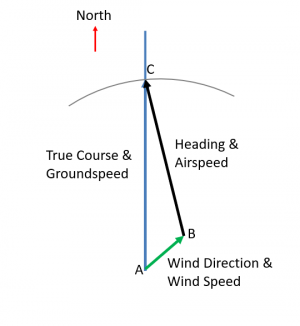
| + | The wind triangle (<xr id='fig:wind-triangle'/>) shows the relationship among the aircraft heading/airspeed, wind direction/speed, and true course/groundspeed. In the most common case, the pilot knows the desired ground track, the aircrafts airspeed, and the wind direction/speed. From this, the pilot would like to know the aircraft heading needed to follow that ground track, and the resulting groundspeed. The key insight is that we can treat wind, airspeed, and groundspeed as vectors and observe that the groundspeed vector is the sum of the windspeed and airspeed vectors as shown in the diagram. | ||
| + | |||
| + | We can graphically construct a wind triangle using paper, pencil, protractor and a ruler to solve for the groundspeed and heading given airspeed, course and wind conditions. This can be done with the following procedure. | ||
| + | |||
| + | # Choose a direction on the paper to be North (heading 000), then use a protractor and straight edge to draw a line from a starting point "A" in that direction. In the example in <xr id='fig:wind-triangle'/>, the true course is 000 degrees. | ||
| + | # Draw a second line departing point A representing the wind. Use the protractor to measure the wind direction, and measure the length using the ruler with an agreed scale for speed (e.g., use 1cm on ruler for 10 knots). This results in point B in the figure. | ||
| + | # Place the ruler with the 0 end at point B, and sweep it until the measurement for the airspeed intersects the true course line drawn in Step 1. For example, if the aircraft is traveling at 100 knots, find the point where 10cm on the ruler intersects the true course line. This becomes the airspeed vector BC as shown in the diagram. | ||
| + | # Measure the angle between BC and true north. This is the heading required to maintain the desired ground track. | ||
| + | # Measure the length of segment AC, this is the resulting groundspeed. | ||
==== GPS Navigation ==== | ==== GPS Navigation ==== | ||
Latest revision as of 16:28, 1 June 2022
SECTION 11. Navigation
Contents
1 Introduction
Air navigation is the process of piloting an airport from one location to a desired location without getting lost, violating airspace restrictions, or endangering the safety of those in the aircraft or on the ground. The specific methods use for navigation depend on many factors including the pilot's experience and familiarity with the route, and the types of navigation equipment available in the aircraft. Methods can include pilotage (navigation by reference to landmarks), dead reckoning (calculating a course based on compass headings and wind conditions), GPS-based navigation, and VOR-based navigation. In addition, some aircraft may be equipped with an autopilot that may or may not interface with the navigation equipment. It is the responsibility of the pilot to become familiar with the equipment available in the aircraft they are operating.
1.1 Pilotage and Dead Reckoning
1.1.1 Pilotage
Pilotage is the process of navigating by reference to fixed points on the ground, often in conjunction with an aeronautical chart or map, or by using the chart to plan the route. It is often the simplest form of navigation and often the first one that a pilot will learn. In SL, pilotage can include flight by reference to specific region names. For example, to fly from White Star Airport (SLWS) to Hollywood (SLHA), one might use the following route:
- Depart SLWS Eastbound
- Turn right to South at Oobilon
- Turn left to East at Blake Sea - Swab
- Turn left to North at Blake Sea - China
- Land at Hollywood
1.1.2 Dead Reckoning
Dead reckoning, in the context of air navigation, is the process of calculating heading, speed and time to travel between fixed points given vehicle speed and wind conditions. While manual dead reckoning is not a common technique for SL navigation, it is useful for pilots to understand the basics, in particular when flying an aircraft with simulated wind.
In the no-wind case, a pilot could simply use an aeronautical chart to measure the heading needed to fly from her current location to her destination, then calculate the time required as the distance divided by the airspeed. For example, to make a 30km flight at an airspeed of 60 kph would require 30 minutes.
The presence of wind, can make things more complicated (for aircraft that support wind). When there is a direct tailwind, we can simply add the windspeed to the airspeed to get groundspeed, and when there is a direct headwind, we can simply subtract the airspeed. In the same example as above, if there is a 10 knot tailwind, then the groundspeed becomes 70 knots, and this the time to cover the 30 km flight would be 30/70 hours or 26 minutes.
Things can be more complicated still when the wind is not aligned with the direction of travel. In this case we must employ the wind triangle to calculate a heading and groundspeed. Before explaining the wind triangle, we make the following definitions:
- True Course - The course from a departure fix to a destination fix.
- Heading - The direction in which the aircraft is "pointing".
- Airspeed - The speed through the air as shown on the airspeed indicator.
- Groundspeed - The actual speed across the ground.
- Wind Correction - The difference between the true course and the heading.
The wind triangle (Figure 1) shows the relationship among the aircraft heading/airspeed, wind direction/speed, and true course/groundspeed. In the most common case, the pilot knows the desired ground track, the aircrafts airspeed, and the wind direction/speed. From this, the pilot would like to know the aircraft heading needed to follow that ground track, and the resulting groundspeed. The key insight is that we can treat wind, airspeed, and groundspeed as vectors and observe that the groundspeed vector is the sum of the windspeed and airspeed vectors as shown in the diagram.
We can graphically construct a wind triangle using paper, pencil, protractor and a ruler to solve for the groundspeed and heading given airspeed, course and wind conditions. This can be done with the following procedure.
- Choose a direction on the paper to be North (heading 000), then use a protractor and straight edge to draw a line from a starting point "A" in that direction. In the example in Figure 1, the true course is 000 degrees.
- Draw a second line departing point A representing the wind. Use the protractor to measure the wind direction, and measure the length using the ruler with an agreed scale for speed (e.g., use 1cm on ruler for 10 knots). This results in point B in the figure.
- Place the ruler with the 0 end at point B, and sweep it until the measurement for the airspeed intersects the true course line drawn in Step 1. For example, if the aircraft is traveling at 100 knots, find the point where 10cm on the ruler intersects the true course line. This becomes the airspeed vector BC as shown in the diagram.
- Measure the angle between BC and true north. This is the heading required to maintain the desired ground track.
- Measure the length of segment AC, this is the resulting groundspeed.